The Essence of Deep Learning: Succinctly Describing Complex Representations

Explaining complexity with simple equations has a certain elegance to it. For this reason, I have always been drawn to physics and pure mathematics. While working on my Ph.D. as a computer engineer, my programming background and interests eventually led me to an interesting hypothesis:

“Parameter efficiency is tied to parameter reuse. All mainstream deep learning models reuse parameters directly or indirectly. Their computational graphs can be horizontally unrolled into a form where this can be shown explicitly. The unrolled size grows exponentially with depth. In this unrolled form, their expected level of parameter reuse (i.e. expected spread) can be quantified using a simple counting approach.”

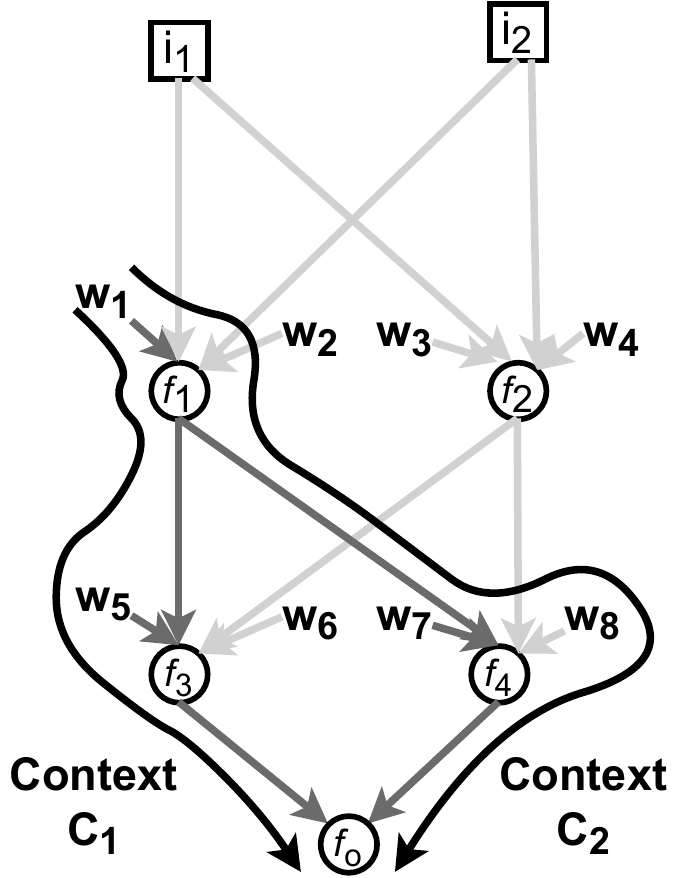
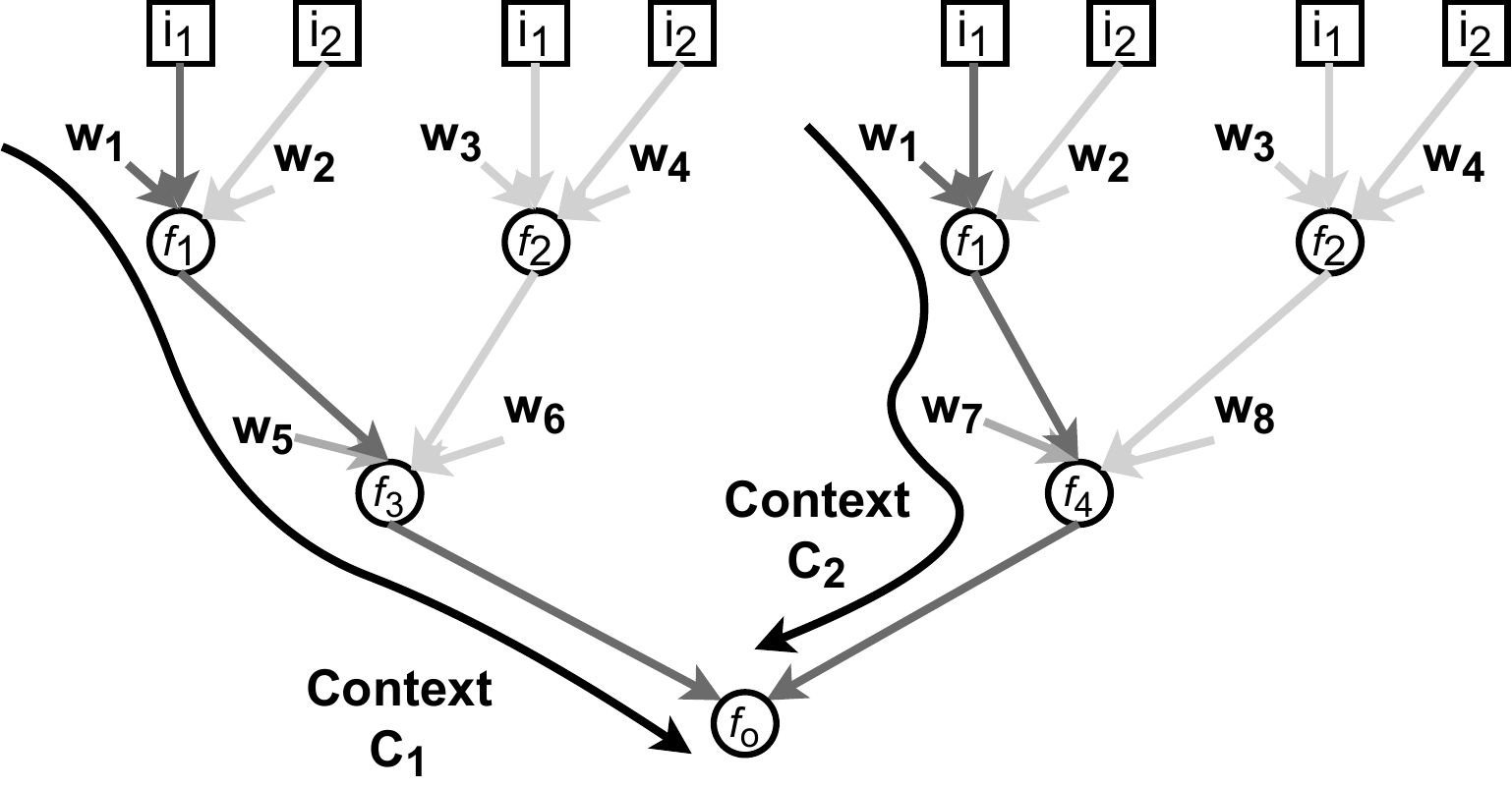
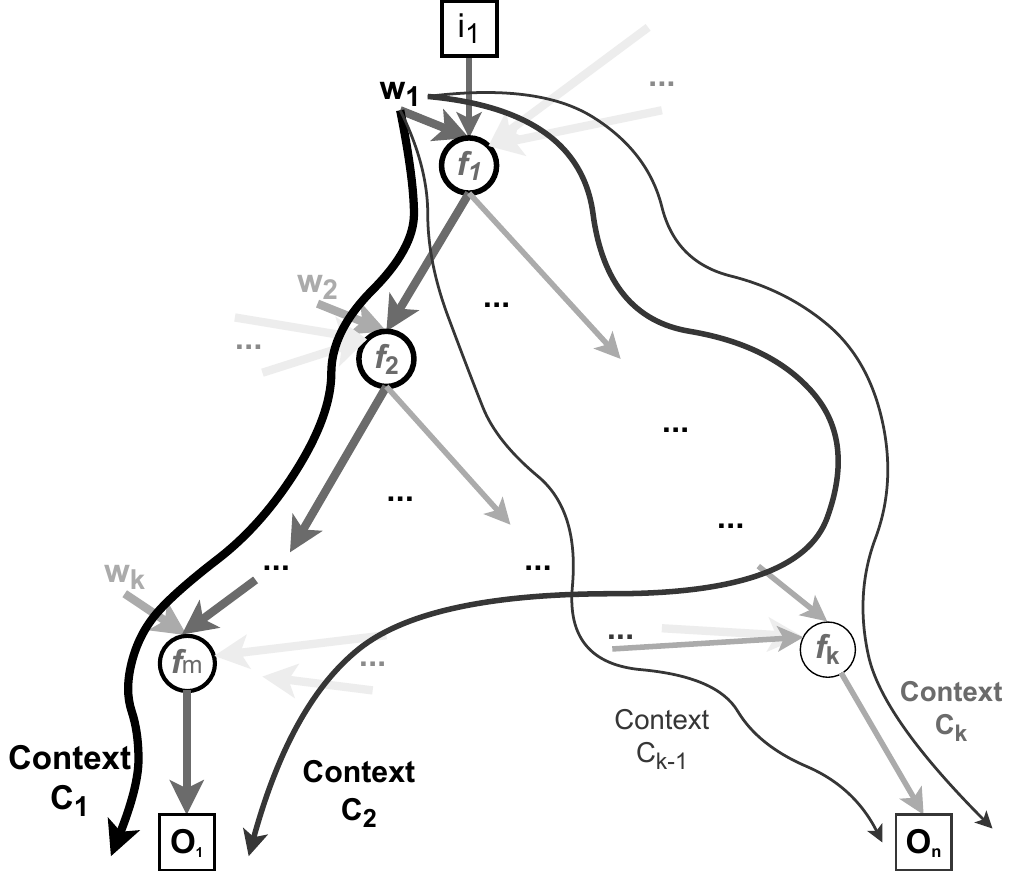
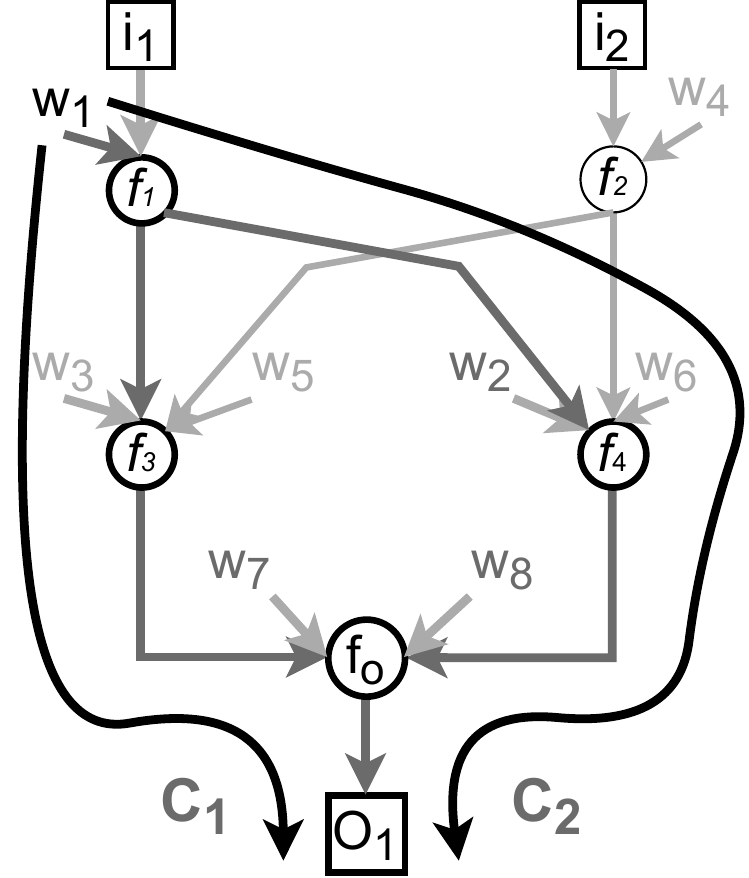
How many different contexts each learnable parameter contribute to in the above graph can be directly counted from the unrolled graph below:

What is a Context?

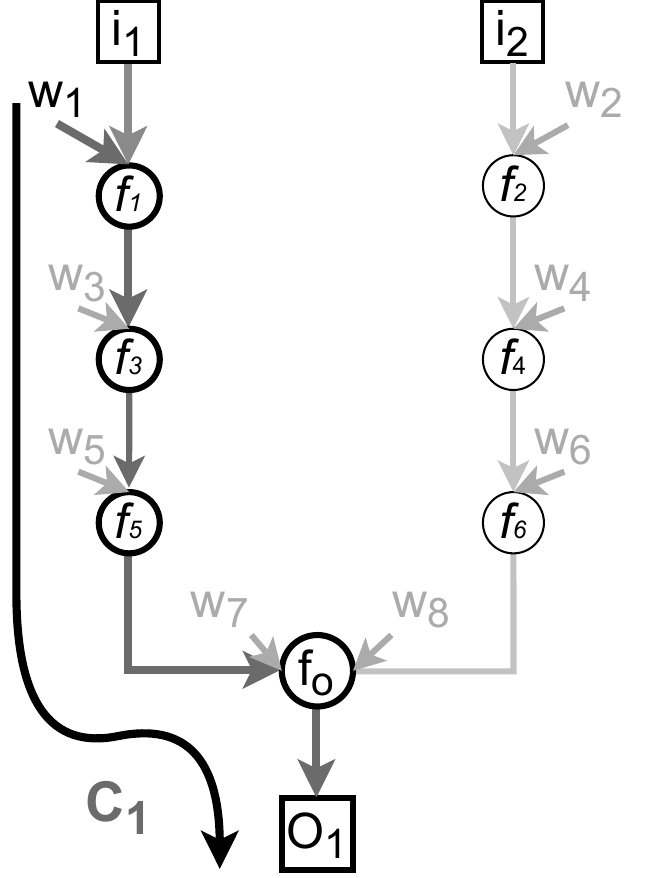
A context is a path from a parameter associated with an input to an output. \(C_1\) is the bold path from \(w_1\) associated with \(i_1\) through functions \(f_1\), \(f_2\), .., \(f_m\) contributing to the output \(O_1\). Note that \(w_1\) can contribute to \(O_1\) through multiple contexts (e.g. \(C_1\) and \(C_2\)). Please see my publication (section 1.1) for a more formal definition.

Reusing Parameters

Above graph has eight learnable parameters. Horizontally unrolling it does not change its size.

This graph also has eight learnable parameters. Yet it has more contexts. That is, horizontally unrolling it increases its size. Based on the reusability prior, this graph does a better job reusing its parameters, so it has a better chance to learn more complex representations (i.e. likely would perform better when other training conditions are fixed).

Down the Rabbit Hole: The Reusability Prior

I define the reusability prior as follows:

“DL model components are forced to function in diverse contexts not only due to the training data, augmentation, and regularization choices, but also due to the model design itself. By relying on the repetition of learnable parameters in multiple contexts, a model can learn to describe an approximation of the desired function more efficiently with fewer parameters.”

Predicting model performance by relying on the number of learnable parameters is a naive approach that does not work when different model designs are compared. The reusability prior gives better results. I have a peer reviewed publication which focuses on the model design aspect and introduces a graph-based methodology to estimate the number of contexts for each learnable parameter. By calculating graph based quantities for estimating model performance, it becomes possible to compare models without training. The idea is more general than the model design level, as a diverse number of contexts for learnable parameters is also achieved via increasing the size of the training data, adding regularization, and data augmentation. Future work on these aspects may result in similar predictive abilities in terms of ranking model performance when other conditions are comparable.

Please cite this research as:

@article{polat10.1088/2632-2153/acc713,
    author = {POLAT, AYDIN and Alpaslan, Ferda},
    journal = {Machine Learning: Science and Technology},
    title = {The reusability prior: comparing deep learning models without training},
    url = {http://iopscience.iop.org/article/10.1088/2632-2153/acc713},
    year = {2023}
}

Connection with Statistical Mechanics

The universe seems to reuse the same fundamental rules of physics over and over again. For instance, the laws of thermodynamics hold not only at the classical level but also at the quantum level. The second law of thermodynamics says that entropy never decreases in a closed system. It is essentially about how information is bound to disperse without disappearing. Information can not disappear in a classical system. Similarly in quantum mechanics, the no hiding theorem says that information can only move from one subsystem to another. Furthermore, the partition function in statistical mechanics is useful for modeling both classical and quantum systems.

The partition function can be used for comparing neural architectures as well. The ideas from statistical mechanics are powerful as they rely on very little number of assumptions. Statistical mechanics predict the macrostates of a given system using the number of microstates for different energy levels. In this way, estimation of macrostates such as entropy and the expected energy of the whole system becomes possible. In my PhD thesis I describe an analogy between statistical mechanics and the aforementioned approach in my previous publication:

Let’s denote the expected spread as \(E[\ln C] = \sum_{i=1}^{N_G} p(w_{i})\ln C_{w_{i}}\) where \(C_{w_i}\) is the cardinality of the set of all contexts for \(w_i\) (e.g. the counts obtained from the horizontally unrolled graph). Assigning energies \(E_i\) in the form of \(\ln C_{w_j}\) to learnable parameters allows utilizing the tools of statistical mechanics for the analysis of computational graphs of DL models. This is analogous to a physical system where the absolute temperature T=-1. In this setting, expected spread becomes identical to the expected energy, by relying on the number of contexts (microstates) for each learnable parameter (energy level), an estimation of various model level quantities (macrostates) is possible.

Beyond the Reusability Prior

Assigning energies \(E_i\) with probabilities that encode arbitrary priors is possible. This allows using the tools from statistical mechanics for other assumptions or constraints for model comparison. For instance, in my PhD thesis in the end of Chapter 5 (pp 102-103), I provided a hypothetical example where probabilities drop with depth and \(E_i\) is linearly increased with depth.

Please cite this as:

@phdthesis{polat_2023, 
    author={Polat, Aydın Göze}, 
    title={The reusability prior in deep learning models}, 
    school={Middle East Technical University}, 
    year={2023},
    pages={102-103} 
}